games101计算机图形学入门 (三)模型、视图、投影
本节课续上一课,上一课我们研究了2D平面的变换,这节课,我们转向到3D的情况,学习,视图(view),投影(projection),正交(orthographic),透视(perspective);
阅读材料:第 6 章(Transformation Matrices),第 6.2、6.4、6.5 节;第 7 章(Viewing)
变换
缩放
\[
\mathbf{S}\left(s_{x}, s_{y}, s_{z}\right)=\left(\begin{array}{cccc}
s_{x} & 0 & 0 & 0 \\
0 & s_{y} & 0 & 0 \\
0 & 0 & s_{z} & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\]
平移
\[
\mathbf{S}\left(s_{x}, s_{y}, s_{z}\right)=\left(\begin{array}{cccc}
s_{x} & 0 & 0 & 0 \\
0 & s_{y} & 0 & 0 \\
0 & 0 & s_{z} & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\]
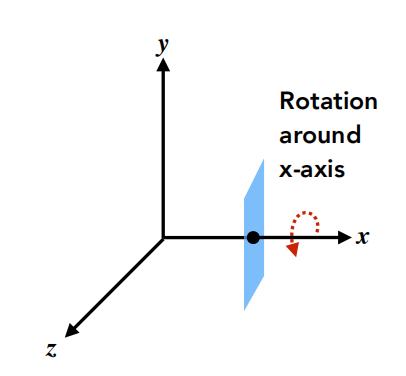
三维之中的旋转
绕x轴
\[
\mathbf{R}_{x}(\alpha)=\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & \cos \alpha & -\sin \alpha & 0 \\
0 & \sin \alpha & \cos \alpha & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\]
绕y轴
\[
\mathbf{R}_{y}(\alpha)=\left(\begin{array}{cccc}
\cos \alpha & 0 & \sin \alpha & 0 \\
0 & 1 & 0 & 0 \\
-\sin \alpha & 0 & \cos \alpha & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\]
绕z轴
\[
\mathbf{R}_{z}(\alpha)=\left(\begin{array}{cccc}
\cos \alpha & -\sin \alpha & 0 & 0 \\
\sin \alpha & \cos \alpha & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\]
ps : 绕哪个轴转,哪个轴的对角线值为1
对于一个任意旋转
大家是否还记得上一节课,我们对于绕任意一点进行旋转的处理呢?
没错,在这里,我们同样借用了上一节的思想,对于绕任意轴旋转这样复杂的变换,我们一定可以将其分解为绕xyz轴旋转矩阵的结合。这样,我们就得到了罗德里德斯旋转公式。
为什么只是简单定义一个向量来表示旋转轴呢?
因为对于任意轴,我们都可以将其平移到原点,在对他进行旋转,所以可以只用一个向量来表示旋转轴
\[
\mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc}
0 & -n_{z} & n_{y} \\
n_{z} & 0 & -n_{x} \\
-n_{y} & n_{x} & 0
\end{array}\right)}_{\mathbf{N}}
\]
ps本课不介绍四元数
四元数在现在也在广泛应用,因为对于这样的一个旋转矩阵,我们是无法进行插值的,而在图形学中,为了将离散的数据连续化,我们会经常使用到插值,以及插值的思想,而四元数,是可以进行插值的
视图(view)
回到我们的主题,学习这些变换,我们是为了处理图形投影之中的一些问题,思考 怎样拍一张照片?
- 安排被拍照人员位置
- 放好相机
- 拍照
在图形学的成像过程,同样也是这样的三部,而第一步就是view(视图变换)
对相机进行定义
- position 位置
\[
\vec{e}
\]
- look at 观察的方向
\[
\hat{g}
\]
- up direction 向上的方向
\[
\hat{t}
\]
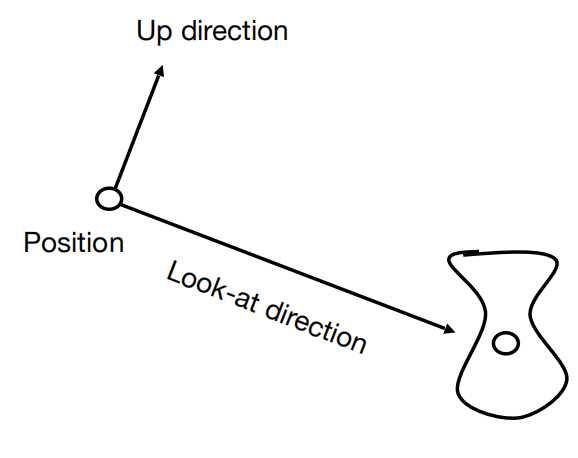
对比物理之中的相对位置,如果2个物体一同移动了同样的位移,那么,2个物体是相对静止的,不变的。那么,我们可以不可以将相机永远放在一个位置?方便我们进行后续的计算。
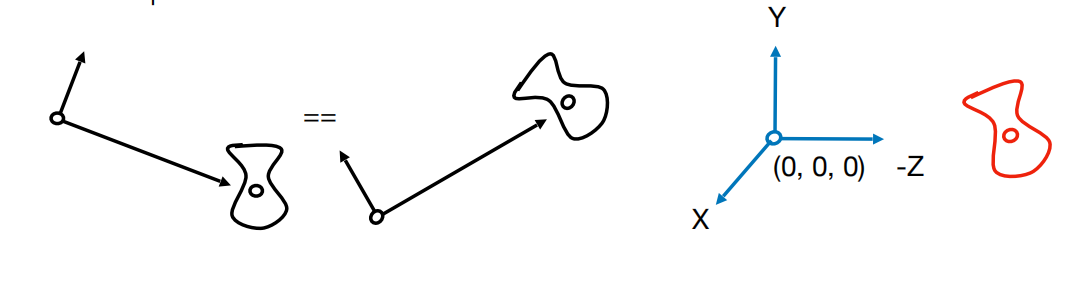
以此作为推论,我们假设让相机永远在原点,相机永远对着-z轴看,相机上方向永远为y轴正方向,那么要怎么操作呢?
- 将相机移动到中心
\[
T_{\text {view }}=\left[\begin{array}{cccc}
1 & 0 & 0 & -x_{e} \\
0 & 1 & 0 & -y_{e} \\
0 & 0 & 1 & -z_{e} \\
0 & 0 & 0 & 1
\end{array}\right]
\]
- 将三个轴,分别旋转到x,y,z
大家可以设想一下,让t旋转到y,g旋转到-z方向,e自然就对到x
很显然,这是可以实现的,但是却不是那么的好写出他的矩阵,我们不如回想一下前一节课的内容:对于二维图形的旋转,没错,我们不需要直接求出该旋转矩阵,我们只需要求出从x->e,y->t,-z->g,在对他进行转置,得到的就是我们需要的矩阵。
\[
R_{v i e w}^{-1}=\left[\begin{array}{cccc}
x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0 \\
y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0 \\
z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\] \[
R_{\text {view }}=\left[\begin{array}{cccc}
x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\
x_{t} & y_{t} & z_{t} & 0 \\
x_{-g} & y_{-g} & z_{-g} & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\]
至此,我们已经可以将摄像机从任意一点移回原点,并且规范化
投影 (projection)
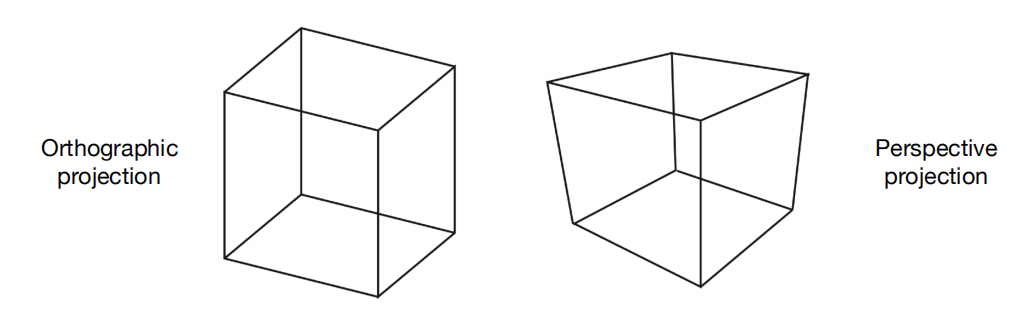
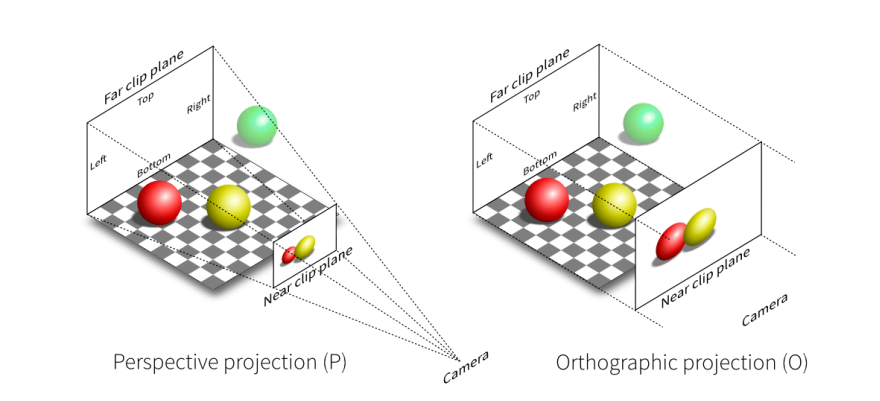
正交投影(orthographic projection) 与 透视投影(perspective projection)
本质 区别:正交投影不会带来近大远小的视觉效果
反应在数学上,我们应该怎么去理解这样的情况呢?
正交投影
对于正交投影,我们有简单粗暴的办法,直接将z值给去掉(用于理解)
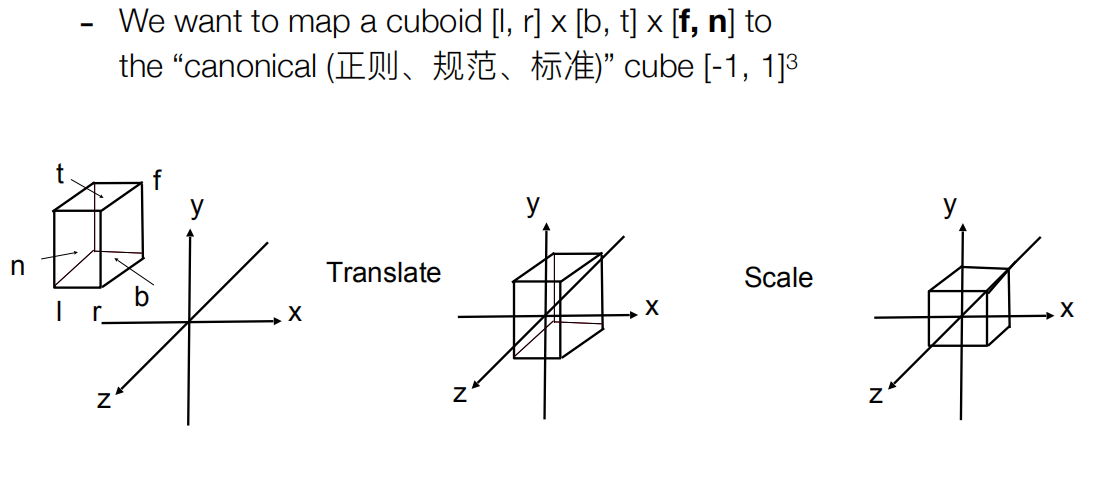
对于图形学,我们用更为直接的方式来实现,给我们一个空间中的长方体,立方体,我们都能对他进行操作,达成正则(规范)化成一个[-1,1]三次方的一个立方体
我们为了方便计算,使得x叉乘y要等于z,使用了右手系。这样带来了一些问题,对于这个图来说,z轴上,我们定义了远近,但是我们面向的是-z方向,z大的离我们进,z小的离我们远。
实际操作的变换矩阵 : 移动到原点,再进行缩放
\[
M_{\text {ortho }}=\left[\begin{array}{cccc}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1
\end{array}\right]
\]
至此,我们实现了正交投影
透视投影
引入:在欧式几何里,我们都知道,平行线是永不相交的,但是,从图形中,我们看到了两条平行线出现了相交,这就是黎曼几何所研究的部分
透视投影和平行投影有什么区别?
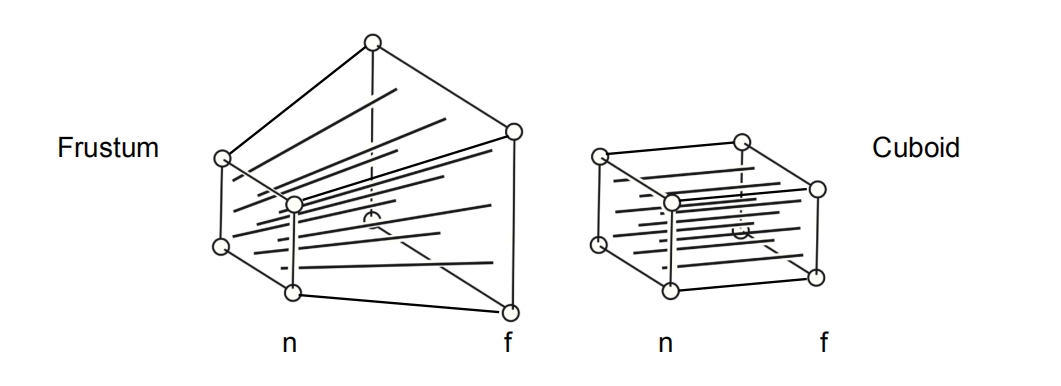
透视投影的远平面比近平面的大小是不一样的,而正交投影的远平面和近平面是一样的。
那么我们是不是想办法先把透视投影转化为正交投影呢?答案是肯定的,只要使得近平面和远平面之间的空间进行挤压,那么我们就能得到透视投影
在得到矩阵前,我们先进行几个定义
- 近平面永远不发生变化
- 远平面的中心点变化后还在中心
- 远平面的z值是不会发生变化的
那么现在,我们就可以开始推导透视变换矩阵了
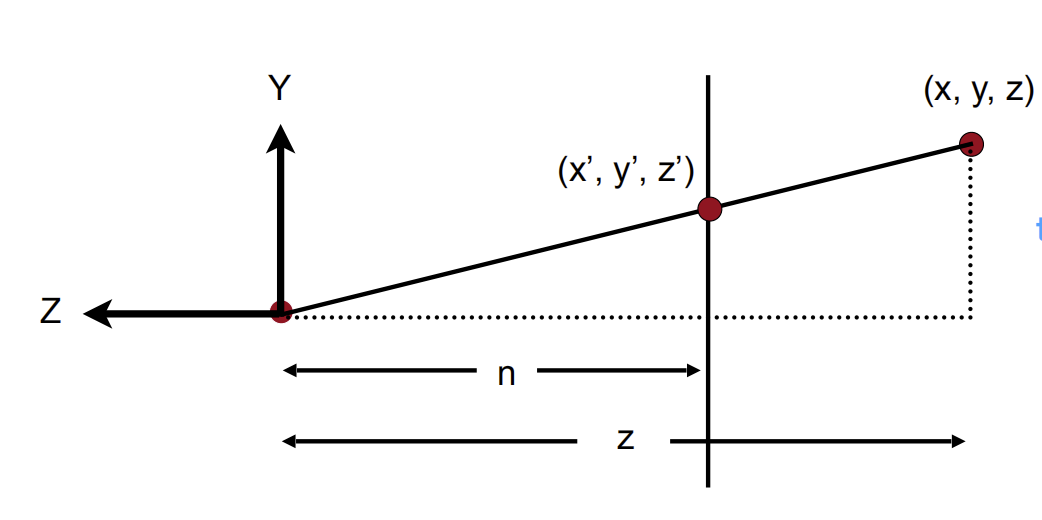
我们观察这个图形,可以,有2个值应该是能很快就可以计算得出的,既x,y的变换,是可以快速推导出的,这个三角形是一个相似三角形,由此推出
\[
y^{\prime}=\frac{n}{z} y \quad x^{\prime}=\frac{n}{z} x
\]
目前,z值的变换就变得非常难以推导。这里,采用猜想的办法,用特定点来推出
\[
\left(\begin{array}{l}
x \\
y \\
z \\
1
\end{array}\right) \Rightarrow\left(\begin{array}{c}
n x / z \\
n y / z \\
\text { unknown } \\
1
\end{array}\right)
\]
我们还记得我们定义的运算可以得出
\[
\Rightarrow\left(\begin{array}{c}
n x \\
n y \\
\text { unknown } \\
z
\end{array}\right)
\]
我们不如从得出的结果,来推导运算的矩阵
第一,二,四行的推导相对容易,因为我们知道,对应的x,y,z的变换
\[
\left(\begin{array}{l}
x \\
y \\
z \\
1
\end{array}\right)\Rightarrow\left(\begin{array}{c}
n x \\
n y \\
\text { unknown } \\
z
\end{array}\right)
\]
从而得到变换矩阵的对应位置
\[
M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0
\end{array}\right)
\]
同样的,第三行不好推导,我们参照定义
因为近平面z是不变的,那么将n带入所以可以得到
\[
\left(\begin{array}{l}
x \\
y \\
n \\
1
\end{array}\right) \Rightarrow\left(\begin{array}{l}
x \\
y \\
n \\
1
\end{array}\right)==\left(\begin{array}{c}
n x \\
n y \\
n^{2} \\
n
\end{array}\right)
\]
可以推导出
\[
\left(\begin{array}{llll}
0 & 0 & A & B
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
n \\
1
\end{array}\right)=n^{2}
\]
同时,对于远平面,处于中点的点进行变换后,仍然处于中点
\[
\left(\begin{array}{l}
0 \\
0 \\
f \\
1
\end{array}\right) \Rightarrow\left(\begin{array}{l}
0 \\
0 \\
f \\
1
\end{array}\right)==\left(\begin{array}{c}
0 \\
0 \\
f^{2} \\
f
\end{array}\right)
\]
那么,对于一个近平面,对于远平面的中心点,我们可以得到这样一个方程组
\[
\begin{array}{l}
A n+B=n^{2} \\
A f+B=f^{2}
\end{array}
\]
解方程组,我们可以得到最后的结果
\[
\begin{array}{l}
A=n+f \\
B=-n f
\end{array}
\]
至此,我们就推导出了完整的一个透视变换矩阵
\[
M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}\right)
\] \[
M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}\right)
\]
Thanks you
图片,课程来源:闫令琪老师的games101计算机图形学入门课程,欢迎大家前去了解







Comments NOTHING